We consider a diffeomorphism 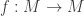 where
where  is a compact manifold.
is a compact manifold.
A topological attractor is a compact subset  which is (i) invariant:
which is (i) invariant:  ; (ii) chain recurrent: for any
; (ii) chain recurrent: for any 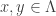 , any
, any 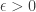 , there exists a finite sequence
, there exists a finite sequence 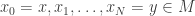 such that
such that  ; and (iii) whose basin,
; and (iii) whose basin, 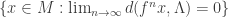 , is a neighborhood of
, is a neighborhood of 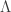 . This last property can be stated as: it admits a neighborhood
. This last property can be stated as: it admits a neighborhood  such that
such that  .
.
One might be tempted to think that any (or almost every) diffeomorphism admits at least one attractor. This is the case on surfaces (according to Pujals-Sambarino) and in higher dimension far from homoclinic tangencies (according to Crovisier-Pujals). However this fails in full generality.
More precisely, in a 2009 preprint, Bonatti, Li and Yang have built, on any compact manifold of dimension at least 3, a locally 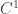 -generic diffeomorphism with no topological attractor (i.e., this property holds for all diffeomorphism in a subset containing a dense intersection of countably many open subsets of some fixed open subset of
-generic diffeomorphism with no topological attractor (i.e., this property holds for all diffeomorphism in a subset containing a dense intersection of countably many open subsets of some fixed open subset of 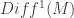 ).
).
Rafael Potrie has explained to our work group (on June 21) his construction of such an example (see the preprint here). His example is derived from Anosov. This allows a precise control of its dynamics:
- there is a unique minimal Milnor attractor. More precisely, it is a compact invariant set which is chain recurrent, whose basin has full Lebesgue measure and such that any invariant proper compact subset has a basin of zero Lebesgue measure.
- each chain recurrent class besides the Milnor attractor is contained in a cycle of center-stable-leaves.
He carefully explained his construction. He starts with a hyperbolic automorphism of the 3-torus with a simple expanding eigenvalue and a pair of conjugate, non-real, contracting eigenvalues. As in Bonatti-Viana’s paper, one modifies it in a ball of some small radius 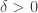 around a fixed point
around a fixed point  to get:
to get:
 becomes a saddle point with one wealky contracting eigenvalues and two expanding ones such that the area of any 2-plane is expanding. Also, its local stable curve has length larger than
becomes a saddle point with one wealky contracting eigenvalues and two expanding ones such that the area of any 2-plane is expanding. Also, its local stable curve has length larger than  ;
;- there are thin unstable, resp., center-stable cones, invariant under
 , resp.,
, resp., 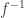 , and close to the unstable, resp. stable, spaces of the linear map.
, and close to the unstable, resp. stable, spaces of the linear map.
According to Bonatti-Viana, there is a constant 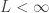 such that, any center-stable disk of radius bigger than
such that, any center-stable disk of radius bigger than 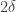 and any unstable curve of length at least
and any unstable curve of length at least  intersect.
intersect.
Recall that a quasi-attractor is a compact subset 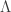 satisfying (i), (ii) and the following weakening version of (iii): it admits a decreasing sequence of neighborhoods
satisfying (i), (ii) and the following weakening version of (iii): it admits a decreasing sequence of neighborhoods 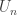 such that
such that 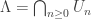 and
and  . An application of Zorn’s Lemma shows that all homeomorphisms of compact sets have quasi-attractors.
. An application of Zorn’s Lemma shows that all homeomorphisms of compact sets have quasi-attractors.
Potrie shows that his diffeomorphism has a unique quasi-attractor by observing that any small piece of unstable curve contained in any 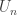 is eventually mapped into a long curve that must meet the large stable disk of a fixed point
is eventually mapped into a long curve that must meet the large stable disk of a fixed point  away from
away from 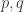 . It follows that any quasi-attractor contains
. It follows that any quasi-attractor contains  . Hence the uniqueness.
. Hence the uniqueness.
To prove that the quasi-attractor is not an attractor, Potrie observes first that it must contains  and that, generically by a result of Bonatti-Crovisier, it must coincide with the homoclinic class of
and that, generically by a result of Bonatti-Crovisier, it must coincide with the homoclinic class of  . The choice of the eigenvalues of the automorphism implies that the center-stable space of this class has no finer dominated splitting.
. The choice of the eigenvalues of the automorphism implies that the center-stable space of this class has no finer dominated splitting.  contracts areas. By Bonatti-Diaz-Pujals, this generically implies that the class is accumulated by sources.
contracts areas. By Bonatti-Diaz-Pujals, this generically implies that the class is accumulated by sources.
The proof that the Milnor attractor is minimal is done in two steps. For  systems, it follows from the existence of a Sinai-Ruelle-Bowen measure. For
systems, it follows from the existence of a Sinai-Ruelle-Bowen measure. For 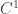 systems, it follows from the fact that the existence of a minimal Milnor attractor supported by the closure of the unstable set of
systems, it follows from the fact that the existence of a minimal Milnor attractor supported by the closure of the unstable set of  is a
is a  , which is dense by the
, which is dense by the  result.
result.
Read Full Post »